Script de Python para calcular la distribución de frecuencias de variables y calcular los parámetros de la ecuación gaussiana que se ajusta a los datos de distribución.

El script usa un fichero de texto con las variables en columnas separadas por tabuladores. Cambia las rutas acorde a tus necesidades. Partimos de D:\bbb\_gausiana-distribucion.txt, un fichero de texto con tantas variables en columnas separadas por tabuladores como deseemos. El script crea, si no existe, la carpeta D:\bbb\_resultados_distribucion y dentro de ella localiza tantos ficheros como columnas tiene D:\bbb\_gausiana-distribucion.txt

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import os

# Crear la función gaussiana para el ajuste: Y=Amplitude*exp(-0.5*((X-Mean)/SD)^2)
def gaussian(x, amplitude, mean, sd):
    return amplitude * np.exp(-0.5 * ((x - mean) / sd) ** 2)

# Ruta del archivo de entrada y del directorio de salida
input_file = r'D:\bbb\_gausiana-distribucion.txt'
output_dir = r'D:\bbb\_resultados_distribucion'

# Crear el directorio de salida si no existe
os.makedirs(output_dir, exist_ok=True)

# Cargar el archivo de datos
data = pd.read_csv(input_file, sep='\t', header=None)  # Cambia sep y header según corresponda

# Inicializar una lista para guardar los resultados de Mean±SD
mean_sd_summary = []

# Inicializar una lista para guardar los datos X e Y en formato de columnas
xy_data_summary = []

# Procesar cada columna
for col in data.columns:
    variable = data[col].dropna()  # Eliminar NaN si los hay

    # Calcular el histograma de frecuencias (sin normalizar)
    counts, bins = np.histogram(variable, bins=30)  # Sin 'density=True' para frecuencia absoluta
    bin_centers = (bins[:-1] + bins[1:]) / 2  # Calcular centros de bins

    # Ajuste de la curva gaussiana
    try:
        popt, _ = curve_fit(gaussian, bin_centers, counts, p0=[1, np.mean(variable), np.std(variable)])
        amplitude, mean, sd = popt

        # Guardar los valores Mean±SD para cada columna
        mean_sd_summary.append(f"Columna {col + 1}: Mean = {mean:.2f} ± {sd:.2f}")

        # Guardar los valores X, Y de frecuencia y Y de ajuste en una lista
        for x, y_hist, y_gauss in zip(bin_centers, counts, gaussian(bin_centers, *popt)):
            xy_data_summary.append([x, y_hist, y_gauss])

        # Guardar los datos x, y del histograma y del ajuste en un archivo CSV
        output_data = pd.DataFrame(xy_data_summary, columns=['X_bin_centers', 'Y_histogram', 'Y_gaussian_fit'])
        output_file = os.path.join(output_dir, f'columna_{col + 1}_frecuencia_ajuste.csv')
        output_data.to_csv(output_file, sep='\t', index=False)

        # Graficar el histograma y el ajuste
        plt.figure()
        plt.hist(variable, bins=30, alpha=0.6, color='skyblue', label='Datos')
        plt.plot(bin_centers, gaussian(bin_centers, *popt), color='orange', 
                 label=f'Ajuste Gaussiano\nAmplitude={amplitude:.2f}, Mean={mean:.2f}, SD={sd:.2f}')
        plt.xlabel('Valor')
        plt.ylabel('Frecuencia Absoluta')  # Cambiar el título del eje Y
        plt.title(f'Distribución de Frecuencias - Columna {col + 1}')
        plt.legend()
        plt.show()

    except RuntimeError:
        print(f"No se pudo ajustar la curva gaussiana para la columna {col + 1}.")

# Mostrar los valores de Mean±SD al final
print("\nResumen de Mean±SD para cada columna:")
for summary in mean_sd_summary:
    print(summary)

# Mostrar los valores X e Y para cada columna en columnas separadas por tabuladores
print("\nValores de X (bin_centers), Y (frecuencia) y Y (ajuste gaussiano) para cada columna:")
for col in data.columns:
    output_file = os.path.join(output_dir, f'columna_{col + 1}_frecuencia_ajuste.csv')
    print(f"\nColumna {col + 1}:")
    print(f"Archivo generado: {output_file}")

Resumen de Mean±SD para cada columna:
Columna 1: Mean = -58.33 ± 6.32
Columna 2: Mean = -63.79 ± 7.14
Columna 3: Mean = -50.60 ± 7.83
Columna 4: Mean = -32.18 ± 5.37
Columna 5: Mean = -15.40 ± 5.42
Columna 6: Mean = -7.57 ± 5.19
Columna 7: Mean = -9.81 ± 5.25
Columna 8: Mean = -2.16 ± 3.55

Valores de X (bin_centers), Y (frecuencia) y Y (ajuste gaussiano) para cada columna:

Columna 1:
Archivo generado: D:\bbb\_resultados_distribucion\columna_1_frecuencia_ajuste.csv

Columna 2:
Archivo generado: D:\bbb\_resultados_distribucion\columna_2_frecuencia_ajuste.csv

Columna 3:
Archivo generado: D:\bbb\_resultados_distribucion\columna_3_frecuencia_ajuste.csv

Columna 4:
Archivo generado: D:\bbb\_resultados_distribucion\columna_4_frecuencia_ajuste.csv

Columna 5:
Archivo generado: D:\bbb\_resultados_distribucion\columna_5_frecuencia_ajuste.csv

Columna 6:
Archivo generado: D:\bbb\_resultados_distribucion\columna_6_frecuencia_ajuste.csv

Columna 7:
Archivo generado: D:\bbb\_resultados_distribucion\columna_7_frecuencia_ajuste.csv

Columna 8:
Archivo generado: D:\bbb\_resultados_distribucion\columna_8_frecuencia_ajuste.csv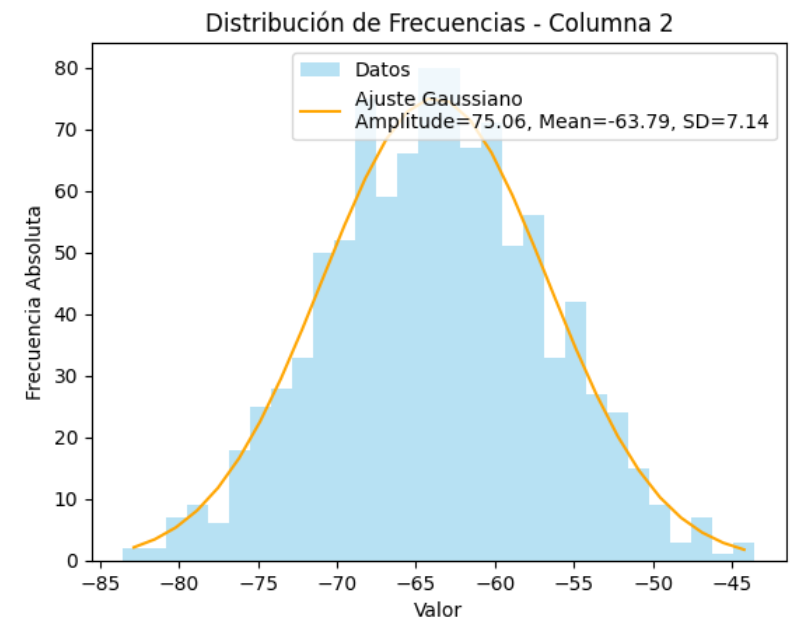

Amplitud es la altura del centro de la distribución en unidades Y.

Media es el valor X en el centro de la distribución.

SD es una medida de la anchura a mitad de altura de la distribución, en las mismas unidades que X.