Rango de valores que cubren un porcentaje central de una distribución gaussiana.

Calcula el rango de valores (límite inferior y superior) que cubren el porcentaje central especificado de una distribución, asumiendo una forma gaussiana. A continuación se muestra un ejemplo de datos generados a partir de una distribución de frecuencias de una variable: Bin Center and # values.

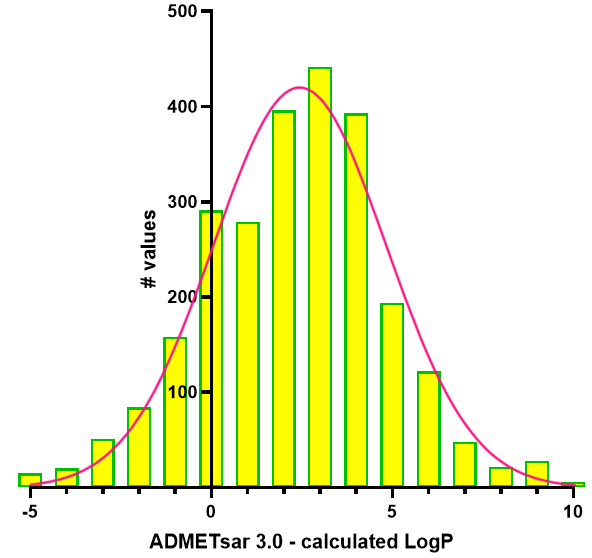
import numpy as np
import scipy.stats as stats
import os

# --- Parámetros de Archivo ---
ARCHIVO_ENTRADA = r'C:\aaa\rango.txt'
ARCHIVO_SALIDA = r'C:\aaa\rango-valores.txt'
NIVEL_CONFIANZA = 0.90 # 90% central

def calcular_rango_gaussiano(archivo_entrada, archivo_salida, confianza):
    """
    Calcula el rango de valores (límite inferior y superior) que cubren el
    porcentaje central especificado de una distribución, asumiendo una forma gaussiana.
    """
    print(f"Iniciando el procesamiento del archivo: {archivo_entrada}")
    
    # 1. Cargar y parsear los datos
    try:
        # Usamos np.loadtxt para leer datos tabulados, ignorando el encabezado si existe
        data = np.loadtxt(archivo_entrada, dtype=float, delimiter='\t', skiprows=1 if os.path.getsize(archivo_entrada) > 0 and open(archivo_entrada).readline().strip().split('\t')[0].isalpha() else 0)
    except FileNotFoundError:
        print(f"Error: El archivo de entrada no se encontró en {archivo_entrada}")
        return
    except Exception as e:
        print(f"Error al leer o parsear el archivo: {e}")
        return

    # Se asume que la columna 0 es 'Bin Center' (X) y la columna 1 es '# values' (Frecuencia)
    if data.ndim < 2 or data.shape[1] < 2:
        print("Error: El archivo debe tener al menos dos columnas (Bin Center y # values).")
        return
        
    bin_centers = data[:, 0]
    frequencies = data[:, 1]
    
    # 2. Generar una lista de valores repetidos para calcular la media y la desviación estándar
    # Esto es necesario para tratar los datos binned como si fueran muestras individuales
    # Ejemplo: Si Bin Center es 2 y Freq es 5, añadimos [2, 2, 2, 2, 2] a la lista
    todos_los_valores = np.repeat(bin_centers, frequencies.astype(int))
    
    if len(todos_los_valores) == 0:
        print("Error: El archivo no contiene valores válidos para el análisis.")
        return

    # 3. Calcular la Media (mu) y la Desviación Estándar (sigma)
    mu = np.mean(todos_los_valores)
    sigma = np.std(todos_los_valores)
    
    # 4. Calcular el Puntuación Z (Z-score) para el nivel de confianza
    # El valor q es (1 - confianza) / 2 para obtener el percentil inferior
    q = (1 - confianza) / 2
    # stats.norm.ppf(q) devuelve el valor Z que deja 'q' área en la cola izquierda
    z_score = stats.norm.ppf(1 - q) 
    
    # 5. Calcular los límites del rango
    limite_inferior = mu - z_score * sigma
    limite_superior = mu + z_score * sigma

    # 6. Escribir los resultados en el archivo de salida
    try:
        with open(archivo_salida, 'w') as f:
            f.write(f"--- Análisis de Rango Gaussiano ---\n")
            f.write(f"Archivo de entrada: {os.path.basename(archivo_entrada)}\n")
            f.write(f"Nivel de Confianza Central: {confianza * 100:.0f}%\n")
            f.write(f"Media Estimada (mu): {mu:.4f}\n")
            f.write(f"Desviación Estándar Estimada (sigma): {sigma:.4f}\n")
            f.write("-" * 35 + "\n")
            f.write(f"Puntuación Z ({confianza * 100:.0f}%): {z_score:.4f}\n")
            f.write(f"Límite Inferior ({q * 100:.1f}%): {limite_inferior:.4f}\n")
            f.write(f"Límite Superior ({(1-q) * 100:.1f}%): {limite_superior:.4f}\n")
            f.write(f"Rango Central ({confianza * 100:.0f}%): {limite_inferior:.4f} a {limite_superior:.4f}\n")
        
        print(f"\nProceso completado. Los resultados se han guardado en: {archivo_salida}")

    except Exception as e:
        print(f"Error al escribir en el archivo de salida: {e}")

if __name__ == '__main__':
    calcular_rango_gaussiano(ARCHIVO_ENTRADA, ARCHIVO_SALIDA, NIVEL_CONFIANZA)

Para los datos anteriores genera unos valores de los extremos: Rango Central (90%): -1.9713 a 6.5665