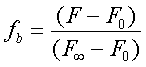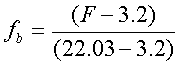ANÁLISIS
MATEMÁTICO DETALLADO DEL CÁLCULO DEL COEFICIENTE
DE PARTICIÓN EN LOS
EXPERIMENTOS DE UNIÓN DE PEPTIDO-NBD A VESICULAS LIPÍDICAS.
Bibliografía: Gazit,
E. y Shai, Y. (1993). Biochemistry.
32: 12363-12371.
Se recoge como ejemplo los datos reales de uno de los
experimentos de unión del péptido ShB-21C-NBD
a vesículas unilamelares pequeñas de PA.
A alicuotas de péptido ShB-21C-NBD de concentración 0.1 mM se le añaden vesículas
unilamelares pequeñas (SUV) de PA
para conseguir distintas relaciones lípido-péptido y se mide la intensidad de
fluorescencia inmediatamente después de la mezcla. La longitud de onda de
excitación es de 470 nm y la de emisión de 530 nm. Se corrige la fluorescencia
de la mezcla ShB-21C-NBD/PA restando
la dispersión de la luz producida por la mezcla ShB-21C/PA. Estos datos iniciales se recogen en la Tabla 1.
Tabla 1: intensidades de
fluorescencia vs relación molar
lípido/péptido
|
PA/
péptido
|
IF530nm de
ShB-21C-NBD---PA
|
IF530nm
de ShB-21C--PA
|
IF530nm
|
|
0.00
|
4.0
|
0.8
|
3.2
|
|
1.38
|
5.63
|
0.81
|
4.82
|
|
2.77
|
6.8
|
0.8
|
6.0
|
|
5.55
|
8.3
|
0.9
|
7.4
|
|
19.45
|
11.5
|
1.0
|
10.5
|
|
33.36
|
13.3
|
1.1
|
12.2
|
|
47.26
|
14.3
|
1.2
|
13.1
|
|
75.08
|
15.4
|
1.2
|
14.2
|
|
103.99
|
16.0
|
1.2
|
14.8
|
|
172.40
|
17.3
|
1.3
|
16.0
|
|
311.60
|
19.0
|
1.4
|
17.6
|
|
450.94
|
20.0
|
1.4
|
18.6
|
|
729.63
|
21.3
|
1.45
|
19.8
|
|
1426.21
|
22.7
|
1.6
|
21.1
|
|
2061.63
|
23.4
|
1.7
|
21.7
|
|
3516.40
|
24.0
|
2.0
|
22.0
|
|
6304.37
|
24.8
|
2.4
|
22.4
|
|
11878.33
|
24.5
|
3.2
|
21.3
|
La representación de estos
datos se recoge en la Fig. 1
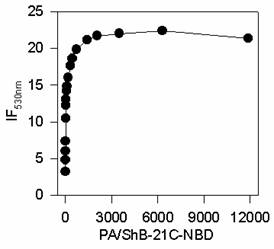
Fig.
1: Curva de unión del péptido ShB-21C-NBD a SUV de PA
Las constantes de unión se
analizan como un equilibrio de partición de acuerdo con la ecuación:
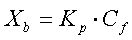
donde Xb se define como la
relación molar del péptido unido (Cb) por lípido total (CL),
Kp
es el coeficiente
de partición, y Cf representa
la concentración
de péptido libre (no unido) en el equilibrio. Para calcular Xb
es necesario conocer primero fb (es decir, la fracción del péptido unido a
membrana), que se calcula utilizando la ecuación:
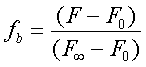
en la que F¥ (la señal de fluorescencia que se obtendría si todo
el péptido se une al lípido), que podría calcularse ajustando los datos los
datos de la Fig. 1 a una ecuación
hiperbólica similar a la que explica la cinética michaeliana o extrapolando a
partir de la representación doble inversa de F (intensidad de la fluorescencia
observada, es decir, IF530nm recogido en la Tabla 1) y de la CL (concentración total de lípido);
equivalente a la representación de Lineweaver-Burk.
El cálculo de F¥ se hará en función de los datos recogidos en la Tabla 2:
Tabla
2: Datos para la representación de dobles inversos.
|
F =IF530nm
|
CL
|
1/F
|
1/CL
|
|
3.2
|
0.0000
|
0.3125
|
+¥
|
|
4.82
|
1.2470e-7
|
0.2075
|
8019246.19
|
|
6.0
|
2.4870e-7
|
0.1667
|
4020908.72
|
|
7.4
|
4.9500e-7
|
0.1351
|
2020202.02
|
|
10.5
|
1.7295e-6
|
0.0952
|
578201.79
|
|
12.2
|
2.9580e-6
|
0.0820
|
338066.26
|
|
13.1
|
4.1806e-6
|
0.0763
|
239200.11
|
|
14.2
|
6.6074e-6
|
0.0704
|
151345.46
|
|
14.8
|
9.1090e-6
|
0.0676
|
109781.53
|
|
16.0
|
1.4918e-5
|
0.0625
|
67033.11
|
|
17.6
|
2.6901e-5
|
0.0568
|
37173.33
|
|
18.6
|
3.8835e-5
|
0.0538
|
25749.96
|
|
19.85
|
6.2537e-5
|
0.0504
|
15990.53
|
|
21.1
|
1.2080e-4
|
0.0474
|
8278.14
|
|
21.7
|
1.7260e-4
|
0.0461
|
5793.74
|
|
22.0
|
2.8768e-4
|
0.0455
|
3476.08
|
|
22.4
|
4.9368e-4
|
0.0446
|
2025.60
|
|
21.3
|
8.5524e-4
|
0.0469
|
1169.26
|
Teniendo que para los
valores pequeños de CL, pequeños errores de F
conducen a grandes errores de 1/F, lo que supondría grandes errores de F¥ , despreciamos los valores más pequeños de la Tabla 2. El valor de la ordenada en el
origen de la ecuación de la recta a la que se ajustan estos puntos será el
inverso de F¥.
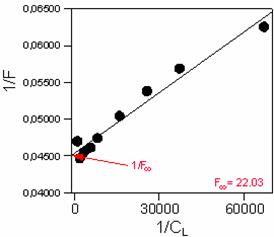
Fig.
2: Representación de dobles inversos para calcular F¥.
Conociendo F¥ podremos calcular la fracción del péptido unido a
membrana (fb):
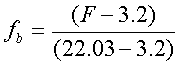
Los datos obtenidos para fb
aparecen en la Tabla 3. En ella
también aparecen los datos de concentración de péptido total (Ct)
(corregidos para el volumen ligeramente distinto en cada relación
lípido-péptido). Multiplicando fb por la concentración de péptido
total obtenemos la concentración de péptido unido (Cb). La
concentración de
péptido libre (Cf) = (Ct)-(Cb). Asumiendo que los péptidos se unen sólo a la
hemicapa externa de los liposomas (60% del lípido total) debemos corregir el
valor de Xb
como:
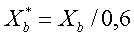
por lo que la ecuación de
partición se convierte en:
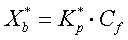
En la Tabla 3 se recogen todos estos parámetros para el ejemplo elegido:
|
fb
|
Ct
|
Cb= fb
x
Ct
|
Cf =Ct
- Cb
|
CL x 0.6
|
Xb* = Cb / CL
x 0.6
|
|
0.0000
|
9.0000e-8
|
0.0000
|
9.0000e-8
|
0.0000
|
---
|
|
0.0861
|
8.9770e-8
|
7.7248e-9
|
8.2045e-8
|
7.4820e-8
|
0.1032
|
|
0.1487
|
8.9550e-8
|
1.3319e-8
|
7.6231e-8
|
1.4922e-7
|
0.0893
|
|
0.2231
|
8.9100e-8
|
1.9878e-8
|
6.9222e-8
|
2.9700e-7
|
0.0669
|
|
0.3878
|
8.8880e-8
|
3.4464e-8
|
5.4416e-8
|
1.0377e-6
|
0.0332
|
|
0.4781
|
8.8670e-8
|
4.2390e-8
|
4.6280e-8
|
1.7748e-6
|
0.0239
|
|
0.5259
|
8.8450e-8
|
4.6513e-8
|
4.1937e-8
|
2.5084e-6
|
0.0185
|
|
0.5843
|
8.8000e-8
|
5.1418e-8
|
3.6582e-8
|
3.9644e-6
|
0.0130
|
|
0.6162
|
8.7590e-8
|
5.3970e-8
|
3.3620e-8
|
5.4654e-6
|
9.8749e-3
|
|
0.6799
|
8.6530e-8
|
5.8833e-8
|
2.7697e-8
|
8.9508e-6
|
6.5729e-3
|
|
0.7649
|
8.6330e-8
|
6.6034e-8
|
2.0296e-8
|
1.6141e-5
|
4.0912e-3
|
|
0.8180
|
8.6120e-8
|
7.0448e-8
|
1.5672e-8
|
2.3301e-5
|
3.0234e-3
|
|
0.8844
|
8.5710e-8
|
7.5803e-8
|
9.9068e-9
|
3.7522e-5
|
2.0202e-3
|
|
0.9508
|
8.4700e-8
|
8.0534e-8
|
4.1662e-9
|
7.2480e-5
|
1.1111e-3
|
|
0.9827
|
8.3720e-8
|
8.2270e-8
|
1.4497e-9
|
1.0356e-4
|
7.9442e-4
|
|
0.9986
|
8.1810e-8
|
8.1697e-8
|
1.1299e-10
|
1.7261e-4
|
4.7331e-4
|
|
1.0199
|
7.8260e-8
|
7.9815e-8
|
-1.5547e-9
|
2.9621e-4
|
2.6945e-4
|
|
0.9614
|
7.2000e-8
|
6.9223e-8
|
2.7766e-9
|
5.1314e-4
|
1.3490e-4
|
La representación Xb*
versus Cf es lo que comunmente
se conoce como isoterma de unión, y que queda representado en la Fig. 3.
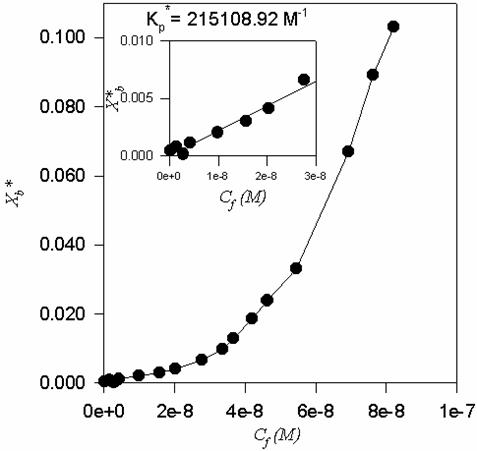
El tramo inicial de la
isoterma de unión se puede ajustar a una recta que pase por el origen, coincide
precisamente con el tramo final o “plato” de la curva de unión (Fig. 1). La pendiente de esta recta
será Kp*
que para el ejemplo tomado tiene un valor de 249.674, 03 M-1.