Laboratorio Integrado I --> SIMULACIÓN 5 --> Estudio del modelo de Hogkin/Huxley del potencial de acción.

INTRODUCCIÓN

En esta práctica se va a estudiar el fundamento iónico del potencial de acción, tomando como base el modelo de Hodgkin-Huxley. El programa simula el movimiento de iones a través de la membrana empleando el mismo procedimiento que en la práctica anterior ("Generación del potencial de membrana").

Dada la rapidez con que tienen lugar los movimientos iónicos durante el potencial de acción, sería necesaria una sonda de permeabilidad muy alta para seguir el curso de las variaciones de potencial de membrana; ello necesitaría intervalos de tiempo muy pequeños para efectuar el cómputo, y la simulación se haría extremadamente lenta. Por ello, el potencial de membrana se calcula en todo momento empleando la ecuación GHK modificada para tener en cuenta el efecto de la ATPasa. Aunque esto constituye una aproximación, ya que puede haber desviaciones apreciables de la situación de estado estacionario, el resultado es cualitativamente realista.

Por otro lado, las permeabilidades del sodio y del potasio no se mantienen constantes, sino que son una función del tiempo y del potencial de membrana, de acuerdo al modelo de Hodgkin-Huxley, y la velocidad de bombeo de la Na⁺, K⁺-ATPasa está ahora de acuerdo a su estequiometría, es decir, se supone proporcional a la tercera potencia de la concentración interna de sodio y a la segunda potencia de la concentración externa de potasio.

LOS PARAMETROS n, m y h .

Con objeto de estudiar de qué manera afectan al perfil del potencial de acción las cinéticas de apertura y cierre de los canales de sodio y de potasio, se ha supuesto que t _n, t _m y t _h varían con el potencial según una gaussiana perfecta, la cual está determinada por los parámetros p₁ p₂ p₃ y p₄. p₄ es el valor constante mínimo; p₃ es la posición del máximo; p₂ la anchura de la gaussiana, y p₁ su altura (la altura total del máximo es por p₁ + p₄). La ecuación de la gaussiana viene dada por:

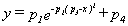
Asimismo, se supone que nµ, mµ y hµ dependen del potencial según una sigmoide perfecta, determinada por los parámetros w₁ y w₂ , de acuerdo a la distribución de Boltzmann y a la influencia del potencial en un proceso que necesita el movimiento de una carga de apertura. w₂ es la posición del punto de inflexión, y w₁ determina la inclinación de la sigmoide (a mayor valor de w₁, más inclinación). La sigmoide viene dada por:

Variando los valores de los parámetros se pueden conseguir diferentes formas del potencial de acción al verse alteradas las constantes cinéticas de apertura y cierre de los canales de sodio y de potasio.

EJECUCION DE LA PRÁCTICA

Se utilizará un programa sencillo de ejecución en MS-DOS. Este programa se ejecuta sobre la aplicación DOSbox. Debes descargar en tu disco duro y descomprimir el fichero DOSBOX.rar sobre el disco C:\ en una carpeta c:\dosbox\

En la figura siguiente puedes ver todos los ficheros y carpetas que se generan después de descomprimir DOSbox.

Para ejecutar DOSbox abre la carpeta DOSbox-0.73 y veras todos los ficheros que contiene, según se muestra en la siguiente figura.

Debes hacer doble click sobre el fichero dosbox.exe y se ejecutará la apertura de un entorno de MS-DOS en el que además está instalado un Windows 3.11. Debes moverte entre directorios con la sintáxis de comandos típica de MS-DOS.

El fichero ejecutable es "potacion.exe". La pantalla inicial de ejecución de este programa se puede ver en la siguiente figura.

OPCIONES DEL PROGRAMA

Al comenzar el programa, aparece un menú de opciones. Teclee el número correspondiente a la opción que desee modificar, en su caso. Las opciones son semejantes al programa de la práctica de estudio del potencial de membrana. El voltaje inicial es el valor del voltaje que utiliza el programa al comenzar el proceso de cómputo. Es un parámetro crítico para la simulación ya que a partir de él se computan los valores iniciales de los parámetros cinéticos de m, h y n, y su valor debe ser igual al del potencial de reposo correspondiente a la distribución iónica de partida, no se recomienda modificar este parámetro en ningún caso. El axón puede estimularse introduciendo un número determinado de variaciones externas en el voltaje, a tiempos determinados, a lo largo de la cinética. La variación externa de voltaje se introduce durante un tiempo equivalente al intervalo de tiempo por iteración. Ello significa que una misma variación de voltaje puede representar un mayor estímulo si aumenta el intervalo de tiempo por iteración. En cuanto a la tabla de concentraciones, cargas y permeabilidades, hay que enfatizar que el programa supone que las tres primeras especies iónicas corresponden al sodio, cloruro y potasio, en este orden, con objeto de procesar los datos adecuadamente. Por ello, no se recomienda modificar el orden de la asignación de especies iónicas. Las permeabilidades de la tabla corresponden a las permeabilidades máximas, de forma que la permeabilidad real (que en este programa tiene el mismo sentido físico que la conductancia), viene dada por el producto de la permeabilidad máxima por n⁴, en el caso del potasio, o por m³h, en el caso del sodio, de acuerdo al modelo HH. Por último, las restantes opciones sirven para modificar los coeficientes w_i correspondientes a los parámetros cinéticos mµ , hµ y nµ y los coeficiente p_i correspondientes a los parámetros cinéticos t _m, t _h y t _n.

El programa representa en la gráfica superior la variación del potencial de membrana, y en la inferior, la variación de la permeabilidad del sodio y del potasio frente al tiempo. Asimismo, se muestran los valores actuales de las concentraciones de cada especie, así como el de los parámetros m, h y n. Con objeto de facilitar la visualización, el valor de estos últimos parámetros también se representa de forma gráfica mediante la barra inferior.

REALIZACIÓN DE LA PRÁCTICA

Estudio general del potencial de acción.- Comience la cinética utilizando las condiciones de partida. Compruebe que el potencial de reposo permanece esencialmente constante. Introduzca un estímulo de algunas decenas de mV a 1 ms. Compruebe que por encima de cierto umbral tiene lugar el potencial de acción, de forma que el proceso es un "todo o nada" y la forma del potencial de acción es siempre la misma. Identifique las diferentes fases del potencial de acción observando la variación de las permeabilidades del sodio y del potasio, así como de los parámetros m, h y n. Determine el potencial umbral del sistema con una precisión de una centésima de mV, a base de probar diferentes estímulos. (Sugerencia: compruebe que si el intervalo de tiempo por iteración aumenta, el potencial umbral disminuye). Introduzca ahora un segundo estímulo de idéntica intensidad algo después del primero, y compruebe que aparece un segundo potencial de acción sólo después del periodo refractario. Determine el periodo refractario del sistema con una precisión de una décima de ms para un determinado estímulo que sea ligeramente superior al potencial umbral.

Estudio de la contribución de los parámetros cinéticos de los canales de sodio y de potasio.- Observe las diferencias obtenidas al aplicar los siguientes cambios, y trate de interpretar los resultados (Retorne a los valores iniciales en cada caso):

• Aumente p₁ de t _ma un valor de 2 e introduzca un estímulo apenas suficiente para provocar un potencial de acción.
• Aumente p₁ de t _n a 10 y provoque un potencial de acción.
• Disminuya, para t _n, p₁ a 0.5 y p₄ a 0.25 y provoque un potencial de acción.
• Disminuya p₃ de t _ha -20 y provoque un potencial de acción.
• Disminuya diez veces los valores de p₁ y p₄ para todos los t , y provoque un potencial de acción.
• Haga w₁ ( mµ ) = 0.09 y w₂ ( mµ ) = -5, y provoque un potencial de acción.
• Idem con w₁ ( nµ ) = 0.1 y w₂ ( nµ ) = -62, y provoque un potencial de acción.

Otros potenciales de acción.- Modifique ahora la concentración de cloruro, asignando 105 mM fuera y 12 mM dentro, y consecuentemente, las del anión indifusible A (45 mM fuera y 138 mM dentro). Modifique, asimismo, el valor de beta(ATPasa) a 2 x 10^-8 , y el valor del voltaje inicial a -65 mV. Ponga en marcha la cinética, en ausencia de estímulos, utilizando una escala de 100 ms y un intervalo de tiempo por iteración de 0.1 ms. Compruebe que el potencial de reposo es estable.

Introduzca ahora un estímulo de 15 mV a 1 ms y deje que la cinética llegue al final. Se llevará una sorpresa. ¿Tiene sentido físico el sistema obtenido? ¿Cuándo acaba la actividad observada? ¿Por qué piensa que puede ocurrir esto?

Estudie el intervalo de tiempo entre el pico de cada potencial de acción. ¿Permanece constante?

Asigne ahora un valor de 3.5 a p₁ (t _n) y de 0.45 a p₄ (t_n). ¿Qué ocurre con el intervalo de tiempo entre cada excitación? ¿Por qué?

Sugerencia: buscar algún cambio de parámetros cinéticos que influyan en esta cinética.